皆さんこんにちは、TaroTechです。
今回はシリーズ第2弾ということで、「推論(順番推理)の解法テクニック」について例題付きで紹介していきます。
推論はSPIの中でも最重要項目であるため難易度もそれなりに高く、SPIの高得点のカギを握っているともいわれているため対策必須の分野になります。
この記事では苦手な人でも解法を自分のものにできるよう、実際に私が解く際に使っているメモ書きを解説として掲載しています。
是非この機会に苦手を克服していきましょう!
1.推論とは?

推論とは、与えられた条件や情報から1つの答えまたは複数の答えを導く問題を指します。
主に就職活動におけるSPIの非言語分野において出題される問題になります。
問題の性質としては、数式を立てて答えを導く単純計算系というよりは、パターンを書き出しながらパズルに当てはめていくようなタイプになります。
時間を掛ければ答えにたどり着けるように、そこまで難解な問題というわけではありません。
しかし、限られた時間の中で正確に処理していくというのが推論の最大の難関ポイントになります。
また、普段から触れる機会の少ないタイプの問題になりますので、ある程度の「慣れ」が必要なのも推論の厄介なところになります。
推論はSPIにおいて頻出の分野でありかつ高得点のカギを握る分野である
始めのうちは難しく感じても、たくさんの問題を解いていく中でしっかり対策して苦手意識をなくしておくことが就活や採用試験において非常に大事になってきます。
2.推論全般の対策・攻略法

ここでは推論全般の対策や攻略法について解説していきます。
2-1.問題パターンごとに解法を知る・覚える
対策・攻略法の1つ目は「問題パターンごとに解法を知る・覚える」です。
ひとえに推論と言ってもいくつかのパターンが存在します。
| 種類 | 重要度 |
|---|---|
| 正誤判断 | |
| 順番推理 | |
| 内訳推理 | |
| 平均推理 | |
| 密度・濃度 | |
| 勝ち負け | |
| 位置関係 | |
| チェックボックス | |
| 数値推理 |
このように推論にはいくつかの問題パターンが存在し、問題ごとに解法や導出までの過程が異なります。それぞれの条件の正誤を判定する問題もあれば、当てはまるものをすべて選ばせるような問題もあります。
学習する過程でそれぞれの解法を知ってさらに覚えることで、問題を解くスピードを上げていくことが大事になります。
是非解法を自分のものにしていきましょう!
2-2.問題文に書かれた情報を式や図に書き起こして整理する
対策・攻略法の2つ目は「問題文に書かれた情報を式や図に書き起こして整理する」です。
推論を素早く正確に解く上でとても大事なのが、情報を整理するということになります。
推論では問題文に多くの情報が書かれており、その情報を基にパターンを書き出しながら問題を解いていくのが一般的です。
もし問題文から読み取ったことを頭だけで考えてしまうと途中でパターンがごちゃごちゃになって結局解けないということになりかねません。
そのため情報を整理して図や式に置き換えながら解答を考えるのが推論を攻略するコツになります。
勉強するときは2色のペンを使って情報を整理するのがおすすめ
推論の問題には1つの問の中で①と②が続いている「組問題」と呼ばれる問題が存在します。
このような問題では①で書きだしたパターンをさらに②で深掘りして答えを導くことになります。
こういった組問題を解く際に、それぞれの問題ごとに使用するペンの色を分けることで情報を色分けするということができます。
そうすることで色ごとに情報が整理され問題を解くスピードを自然と上げつつ正確に解く練習ができるのです。
2-3.学習するときは時間がかかってでも自力で答えまで導出する
対策・攻略法の3つ目は「学習するときは時間がかかってでも自力で答えまで導出する」です。
そもそも学習の時に自力で解くことができなければ、本番でも答えにたどり着くことは不可能です。
逆に言えば時間がかかってでも自力で答えを導き出せるということは、推論を解く能力は備わっているということになるので、後はスピードを上げる訓練をするだけということになります。
最初は模範解答に頼りながら答えまでの過程を真似してもいいので、少しずつ答えを見ないで解くという方式にシフトしていけるとよいでしょう。
このように練習でしっかり自分で解くという癖をつけておけば、本番で初見の問題が出ても、身に着けた解法通り答えを導いて高得点を得ることができるようになります。
2-4.学習が進んだらひたすら問題演習と実践を積むこと
対策・攻略法の4つ目は「学習が進んだらひたすら問題演習と実践を積むこと」です。
結局のところ推論はたくさん問題を解いて慣れることが一番大事になります。
ある程度解法のインプットが終わったら、あとは問題集や実際にテストセンターで受験することをおすすめします。

私も問題集を買って徹底的にアウトプットをし続けていたら、いつの間にか推論が得意になっていました。
【おすすめ問題集】
どちらか1冊を買って何周か問題を解くことを推奨します。
【おすすめのサービス】
おすすめ度:
費用:2500円/6か月
SMART/SPI-Gでは、SPIを実際に自分のパソコンやスマホから本番さながらに演習することができるサービスになります。
メインターゲットは転職者ですが、ラインナップはSPIだけでなく玉手箱も含まれているため就活生にもおすすめです。就活仲間と割り勘して半年間問題演習するとよいでしょう。
4.推論(順番推理)の例題と解答
この記事では推論(順番推理)の例題と解答を紹介していきます。
まず自力で問題を解いてみよう!
例題
【問1】
P、Q、R、Sの4人がテストを受けた。4人の得点についてア、イ、ウが分かっているとき、4人の得点を高い順に並べたものはどれか。
ア Rの得点はPとQの得点の平均に等しい
イ SはPより得点が高いが、1位ではない
ウ Qの次に点が高いのはRではなくSである
A QSRP
B RQSP
C QSPR
D RSPQ
【問2】
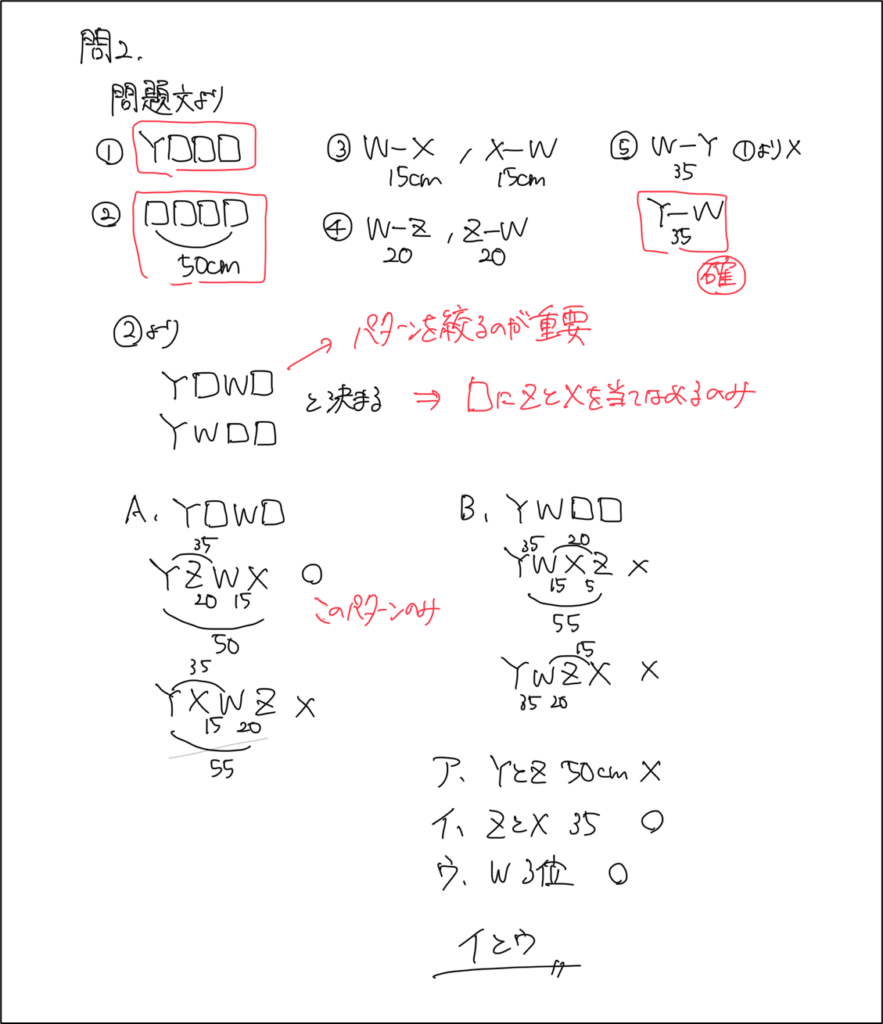
W、X、Y、Zの4人が走り幅跳びをした。1位はYで、1位と4位の差は50cmだった。また、WとXの差は15cm、WとZの差は20cm、WとYの差は35cmだった。
次のうち正しいのはどれか。
ア YとZの差は50cm
イ XとZの差は35cm
ウ Wは3位である
【問3】
W、X、Y、Zの4人が100点満点のテストを受けた。4人の得点について、次のことが分かっている。
Ⅰ) Wの得点はYより5点高い
Ⅱ) WとXの得点の平均は、YとZの平均より5点高い
①Ⅰ)とⅡ)の情報から推論した次のア、イの正誤を答えよ。
ア Xの得点はZより5点高い
イ 4人の中に、同じ得点の人はいない
②上記の情報に加えて次のことが分かった。
Ⅲ) Xの得点は、Yより5点低い
Ⅰ)~Ⅲ)の情報から推論した次のウ、エの正誤を答えよ。
ウ Zの得点は最も低い
エ 4人の中に、同じ得点の人はいない
【問4】
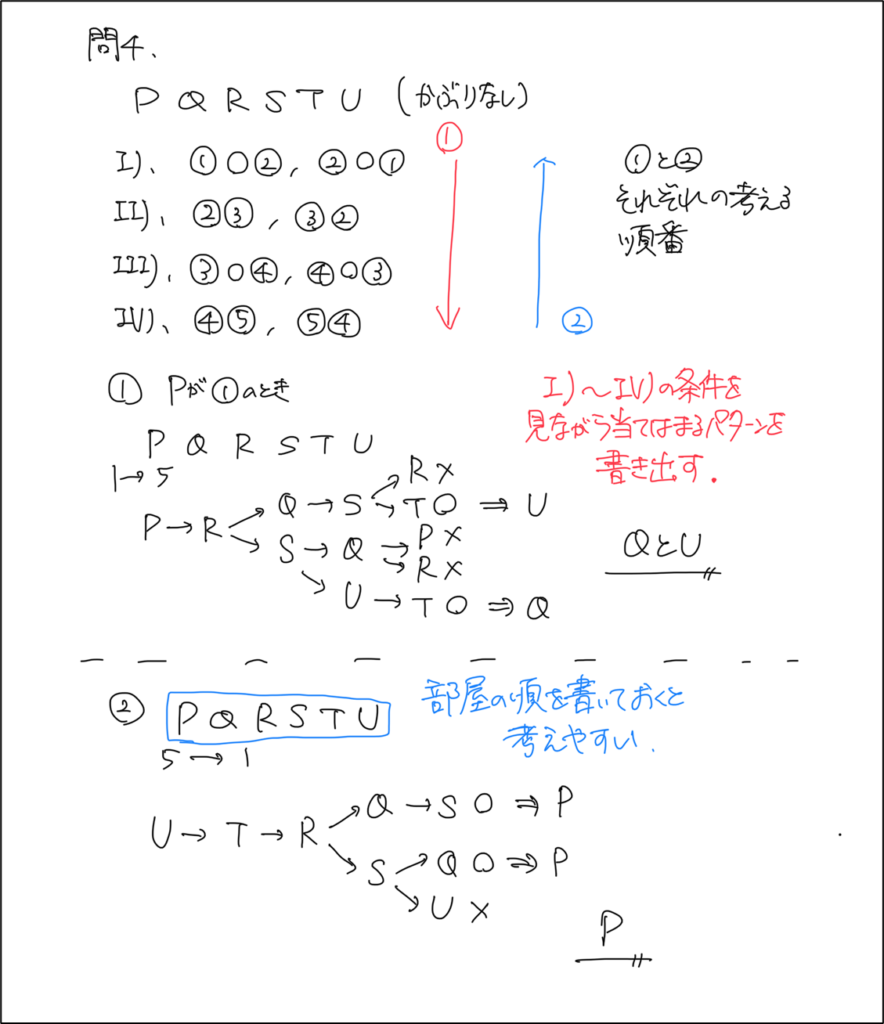
P、Q、R、S、T、Uの6人の部屋がこの順に並んでいる。このうち5人に、配送業者が荷物を1つずつ届けた。配達した順番について、次のことが分かっている。
Ⅰ) 最初に配達した部屋と2番目の部屋の間に1つ部屋がある
Ⅱ) 2番目と3番目に配達した部屋は隣り合っている
Ⅲ) 3番目と4番目の部屋の間に1つ部屋がある
Ⅳ) 4番目と最後の部屋は隣り合っている
①最初に配達した部屋がPの場合、荷物が配達されなかった部屋として当てはまるものをすべて選べ。
②最後に配達した部屋がUだった場合、荷物が配達されなかった部屋として当てはまるものをすべて選べ。
【問5】
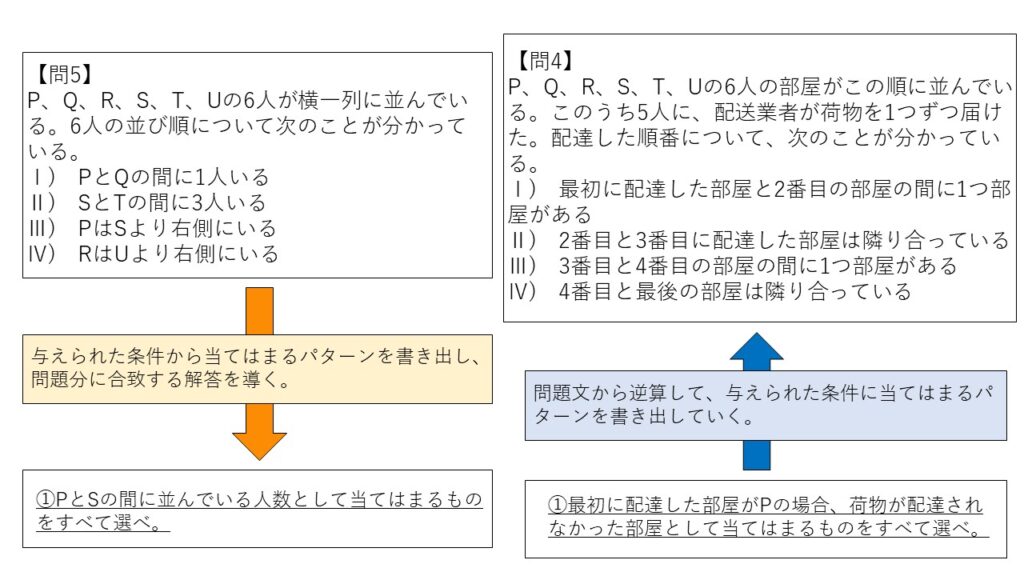
P、Q、R、S、T、Uの6人が横一列に並んでいる。6人の並び順について次のことが分かっている。
Ⅰ) PとQの間に1人いる
Ⅱ) SとTの間に3人いる
Ⅲ) PはSより右側にいる
Ⅳ) RはUより右側にいる
①PとSの間に並んでいる人数として当てはまるものをすべて選べ。
②右端がQの場合、左端に並んでいる人として当てはまる人をすべて選べ。
解答
問1. A
問2. イとウ
問3. ①ア:〇、イ:× ②ウ:〇、エ:〇
問4. ①Q、U ②P
問5. ①0、2、4人 ②S



5.推論(順番推理)の解法テクニック

それでは最後に推論(順番推理)の解法テクニックについて紹介します。
順番パターンをすべて書き出す
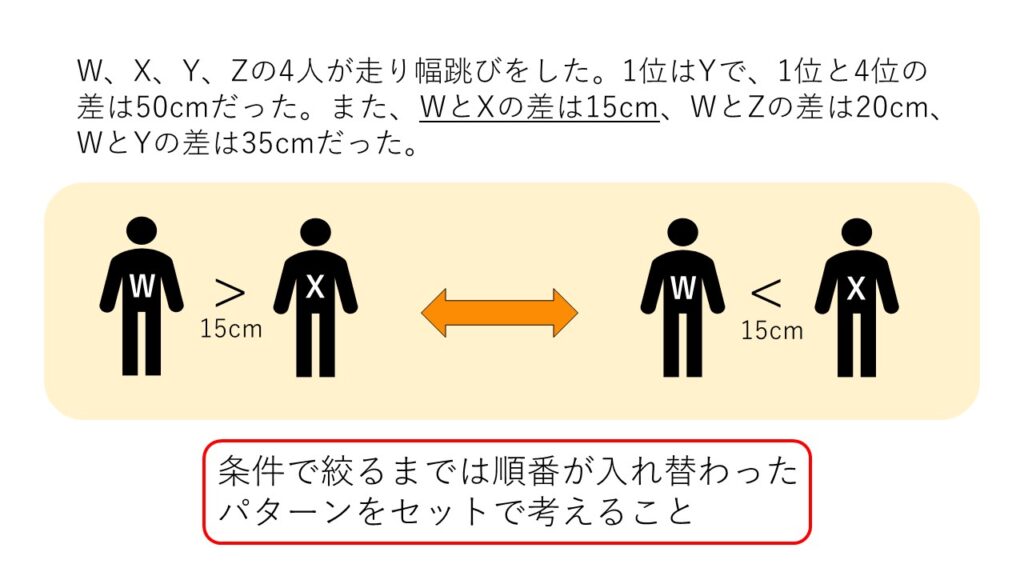
順番推理のテクニック1つ目は「順番パターンをすべて書き出す」です。
この種類の問題を解く際は、それぞれの大小関係や前後関係が重要になってきます。
例えば図のように「WとXの差は15cm」という条件があれば、必ずWが大きい場合とXが大きい場合の両パターンを想定することが重要です。
このように順番推理の問題を解く際は、まず与えられた条件に当てはまる順番のパターンをすべて書き出すという作業をしましょう。
条件同士の整合性を確認しパターンを絞る
順番パターンが書き出せたら、次に、条件同士の整合性を確認しパターンを絞っていきましょう。
書き出したパターンをすべて調べてみれば問題を解くことはできますが、推論は制限時間との戦いでもあるので、あまり効率的な解法ではありません。
そこで重要になってくるテクニックが「パターンを絞る」ということになります。
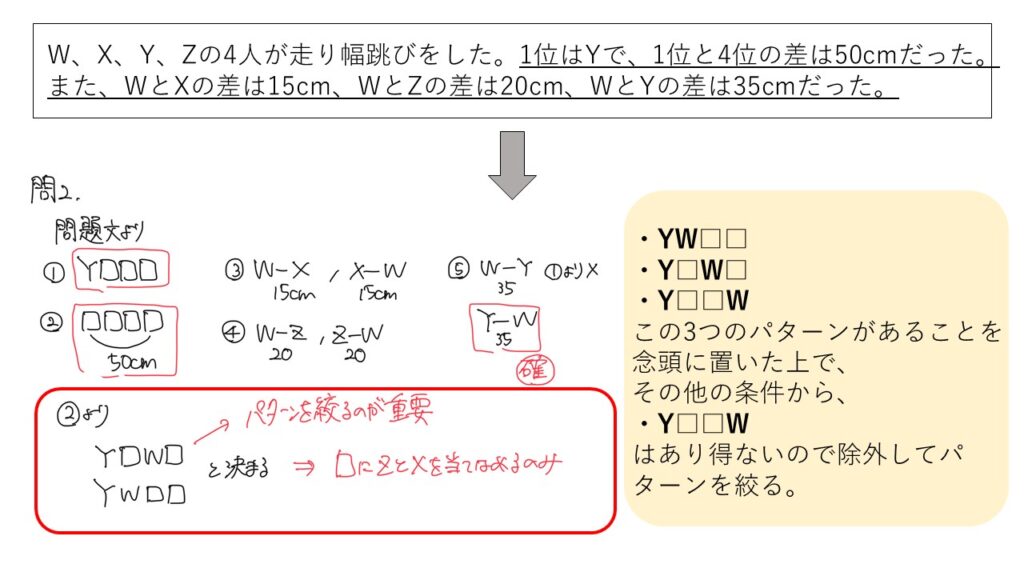
図のようにあらかじめすべてのパターンを念頭においた上で、ほかの条件との整合性を確認し、あり得ないパターンは除外します。
こうすることで最初の段階よりも少ないパターンで答えを導きだすことができるようになります。
ここまでできれば、あとは絞ったパターンの中でさらに条件に当てはまるパターンを書き出していくと答えに辿りつけるでしょう。

例題の問1、2、5あたりはこのテクニックで解答できるタイプの問題だと思います。
問題文から逆算してパターンを書き出す
最後に紹介するテクニックは「問題文から逆算してパターンを書き出す」です。
これは少し特殊パターンになります。
【問4】
P、Q、R、S、T、Uの6人の部屋がこの順に並んでいる。このうち5人に、配送業者が荷物を1つずつ届けた。配達した順番について、次のことが分かっている。
Ⅰ) 最初に配達した部屋と2番目の部屋の間に1つ部屋がある
Ⅱ) 2番目と3番目に配達した部屋は隣り合っている
Ⅲ) 3番目と4番目の部屋の間に1つ部屋がある
Ⅳ) 4番目と最後の部屋は隣り合っている
①最初に配達した部屋がPの場合、荷物が配達されなかった部屋として当てはまるものをすべて選べ。
②最後に配達した部屋がUだった場合、荷物が配達されなかった部屋として当てはまるものをすべて選べ。
例えばこの問題では、Ⅰ)~Ⅳ)に当てはまる並びを書き出して解くこともできますが、その方法だと少し難しくなります。(※下にNG例を掲載)
そこで問題文から解答していくというテクニックを使います。
具体的には、Ⅰ)~Ⅳ)の情報を書き出したうえで、問題文の「最初に配達した部屋がPの場合 」という情報から Ⅰ)~Ⅳ) に当てはまるパターンを書き出していくという解法になります。
ちなみに条件から素直に当てはまるパターンを書き出していく解法だと、

このように解答までが煩雑になってしまい、時間がかかってしまいます。
問題文に条件が指定されている場合は、問題文から逆算して解答することを覚えておくと効率よく問題が解けるようになります。

例題の問4や問5-②がこのパターンに当てはまります。再度復習する場合や似た問題を解く時に実践してみましょう。
まとめ
皆さんいかがだったでしょうか?
今回は推論の攻略法~順番推理編~ということで、例題とともに解法テクニックを紹介してきました。
推論は始めは難しくても、学習を積み重ねているうちに少しずつ問題に慣れてきます。
ぜひ今回紹介した解法テクニックを駆使して高得点を狙っていきましょう!



コメント